Project Description
My final electromagnetic software version is called CSEMoMatic - Omnium. The Latin word ‘Omnium’ was chosen because it roughly translates in English to “for all”. The CSEMoMatic software has publically integrated Dipole1D (Key, 2009a) and AMIRA’s 3D Integral Equation Marco (Xiong, 1992) algorithms. A number of proprietary algorithms have been developed and integrated into a proprietary versions including Hursan and Zhdanov (2002) 3D integral equation algorithm INTEM3D, a quasi-analytical inversion algorithm QAINV (Zhdanov et al., 2000) and a 2.5D irregular finite difference modelling Otze (Scholl and Sinkevich, 2012). Considerable work has been placed into CSEMoMatic. Overall approximately 100,000 lines of Java code have been written by myself for all the versions of CSEMoMatic.
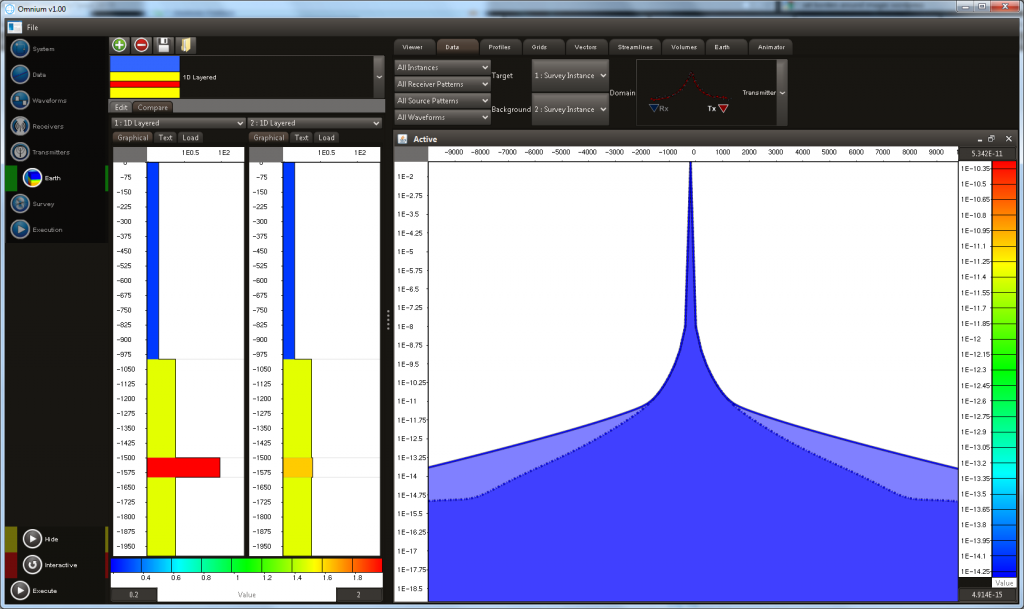
- 1D CSEM Synthetic Profiles of Ex Amplitudes for two models (i) With Hydrocarbon (ii) Without Hydrocarbon
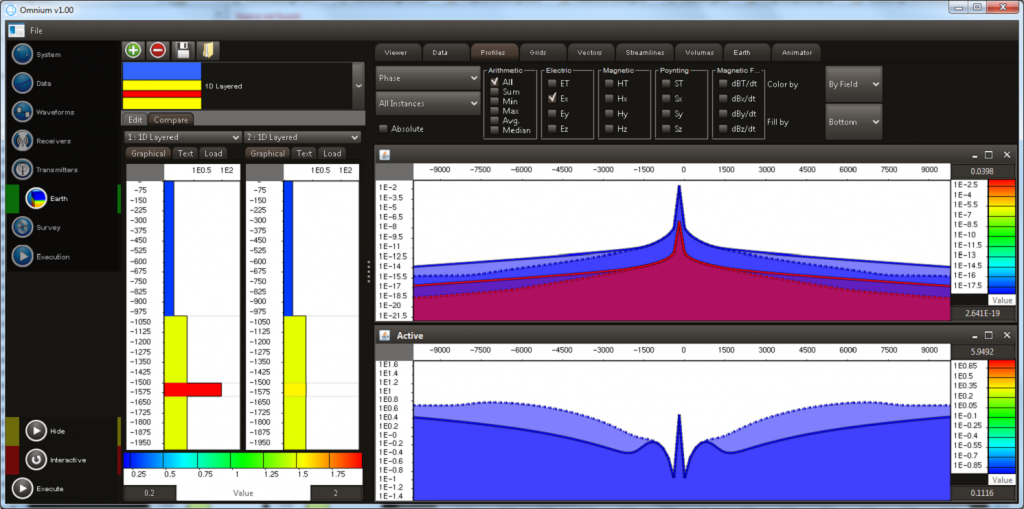
- 1D CSEM Synthetic Profiles of Ex Amplitude and Phase for two models (i) With Hydrocarbon (ii) Without Hydrocarbon. CSEMoMatic Omnium allows multiple panels to be created.
- It also allows multiple transmitter positions to be compared.
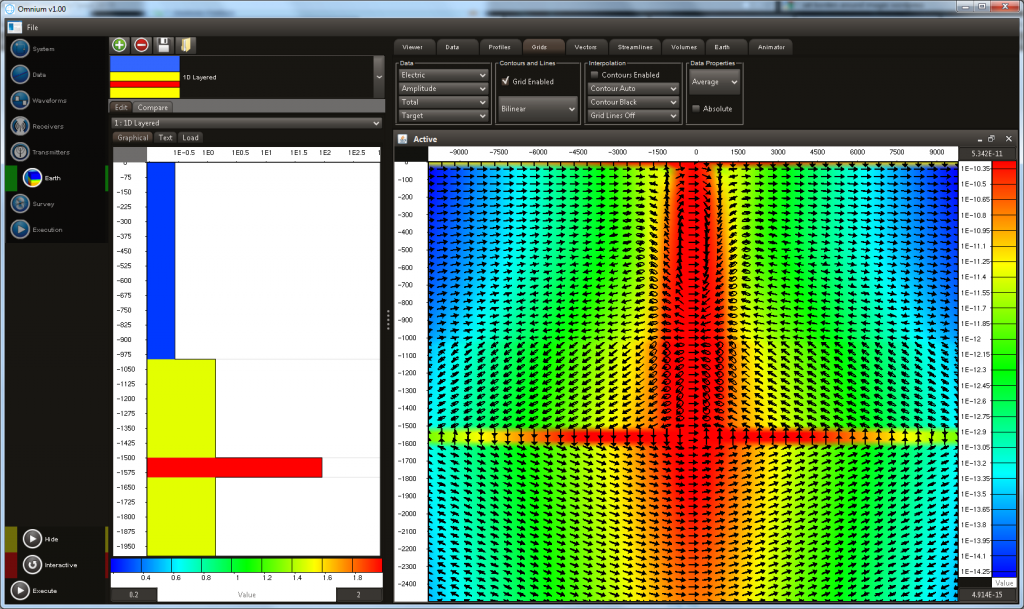
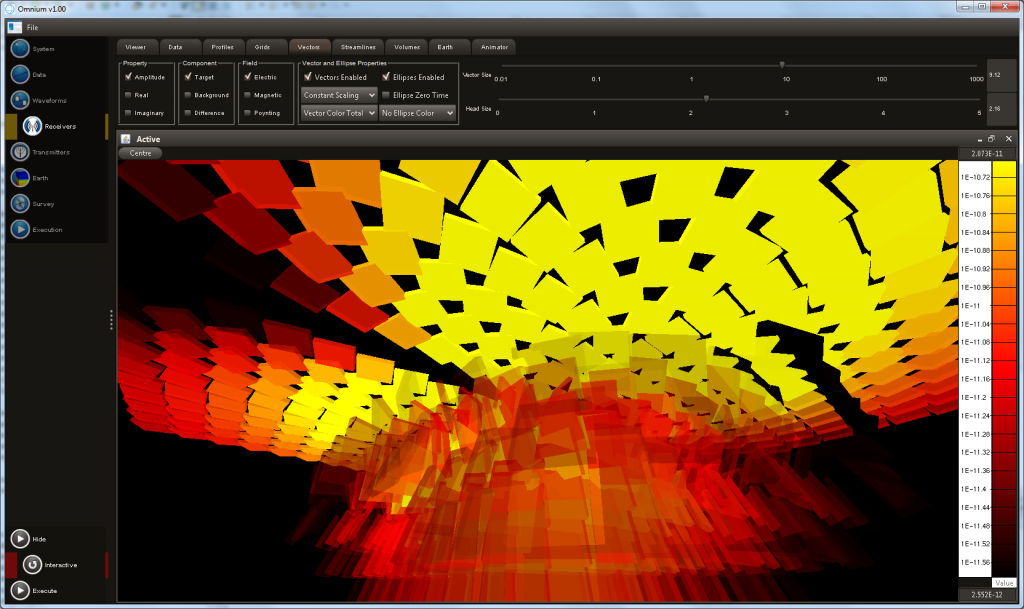
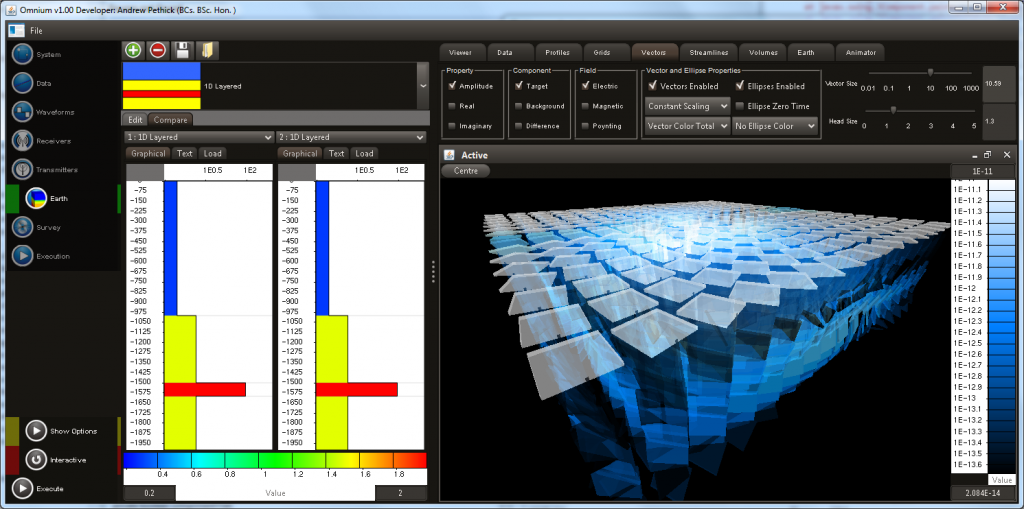
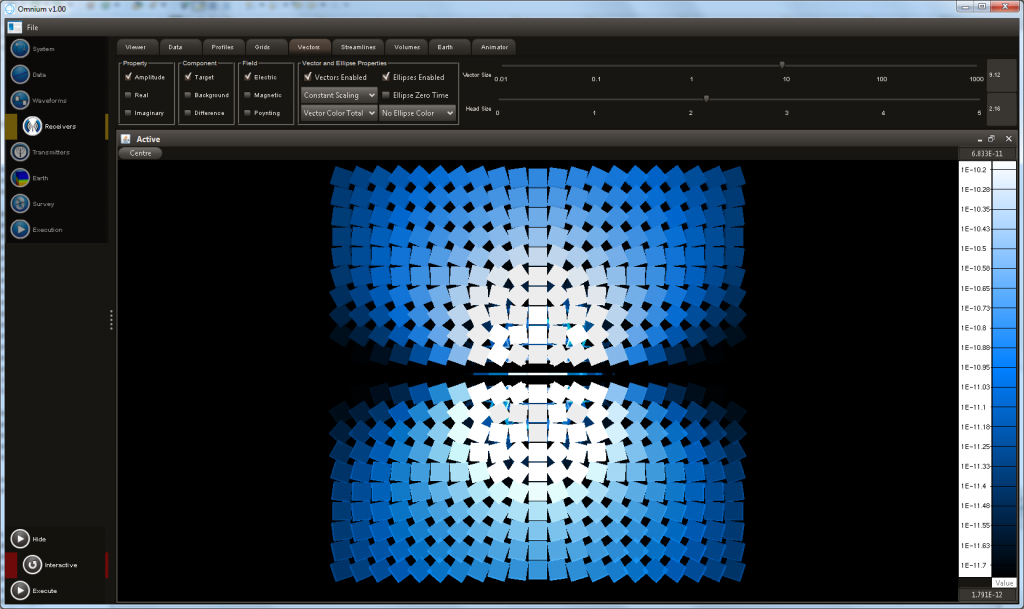
- 2D grids of any electromagnetic field property can be visualised. Vector elements displaying vector orientation can also be displayed. This image shows electric field vectors and electric field polarisation ellipses.
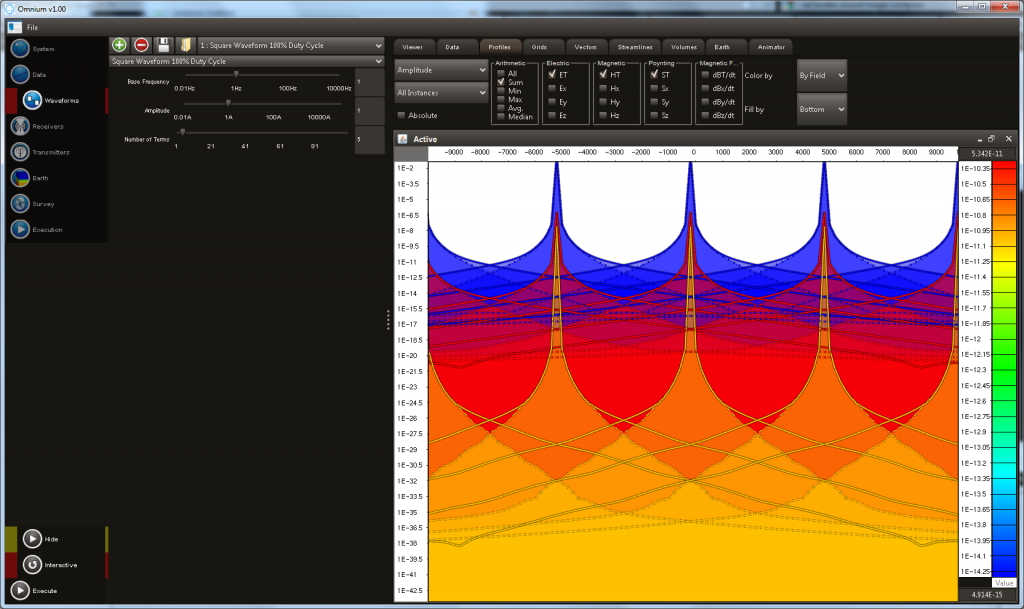
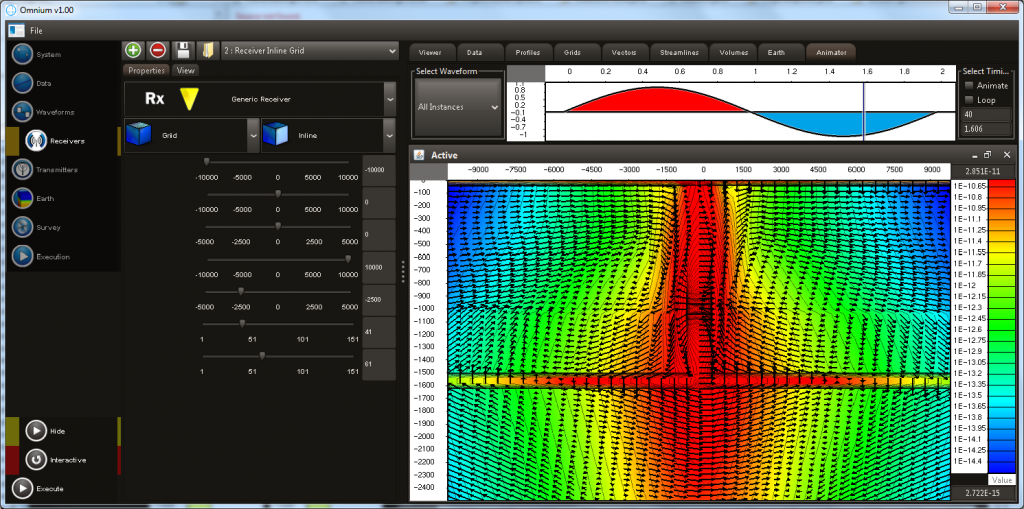
- The electromagnetic field at any point in time can be visualised.
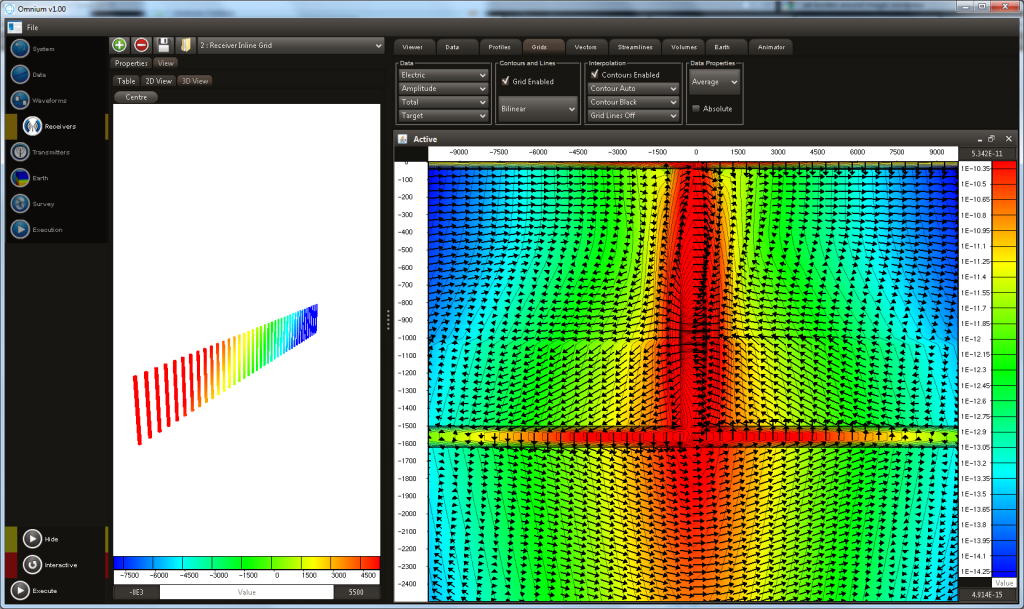
- The survey geometry can also be shown in a 3D viewer
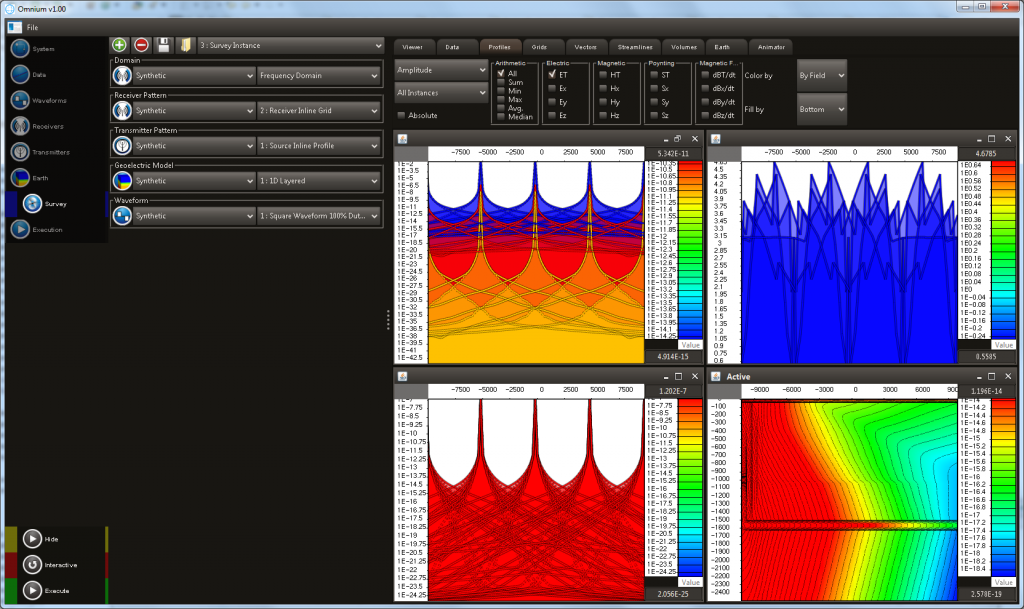
- Multi-panel displays allows multiple dataset to be compared and contrasted
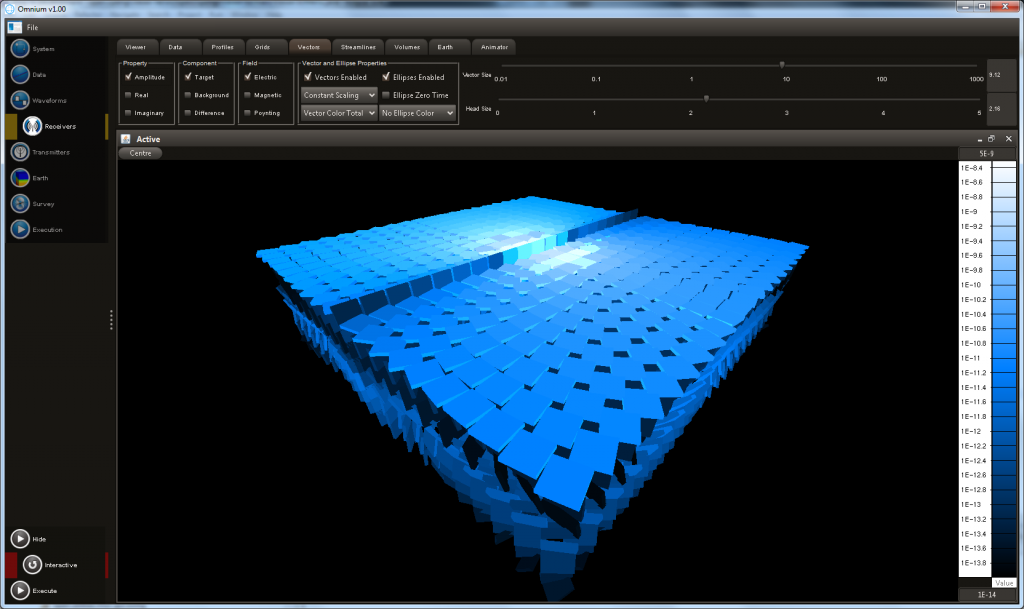
- Synthetic 3D data can be modelled and visualised using technology derived from Java OpenGL
- Multiple lighting and colour options are available.
- Transparency Opaque
- Transparency by amplitude
- Alternative 3D rotation
- Alternative 3D rotation (Plan)
References
- Hursan, G. and M. S. Zhdanov (2002). Contraction integral equation method in three-dimensional electromagnetic modeling. Radio Sci. 37 (6), 1089.
- Key, K. (2009a). 1d inversion of multicomponent, multifrequency marine CSEM data: Methodology and synthetic studies for resolving thin resistive layers. Geophysics 74 (2),
F9–F20. - Scholl, C. and V. Sinkevich (2012). Modeling mcsem data with a finite difference approach and an and unstructured model grid in the presence of bathymetry.
- Xiong, Z. (1992). Electromagnetic modeling of 3d structures by the method of system iteration using integral equations. Geophysics 57 (12), 1556–1561.
- Zhdanov, M. S., V. I. Dmitriev, S. Fang, and G. Hursan (2000). Quasi-analytical approximations and series in electromagnetic modeling. Geophysics 65 (6), 1746–1757.

Recent Comments